Google CTF 2019 - FriendSpaceBookPlusAllAccessRedPremium.com
#MemeFreeEdition
The Challenge
You are provided a zip file containing two files.
programvm.py
The file program contains instructions encoded as emojis for a virtual machine called vm.py.
At the bottom of vm.py I found a list, or lets call it a translation table, with emojis and their function name counter part.
OPERATIONS = {
'🍡': add,
'🤡': clone,
'📐': divide,
'😲': if_zero,
'😄': if_not_zero,
'🏀': jump_to,
'🚛': load,
'📬': modulo,
'⭐': multiply,
'🍿': pop,
'📤': pop_out,
'🎤': print_top,
'📥': push,
'🔪': sub,
'🌓': xor,
'⛰': jump_top,
'⌛': exit
}
To execute program with vm.py I ran:
$ python vm.py program
http://^C
The program started printing letters to the terminal, but became horribly slow, until I decided to terminate the execution.
So the challenge seemed to be, to convince program to give me its secret. With the first characters looking like an URL, the flag might be hidden within the URL or on the website the URL pointing to.
In which way I had to convince the program to reveal its secrets to me, I had yet to decide.
One way could be to optimize the VM code, the other might be optimizing the code of program.
The Solution(s)
Solving the Challenge: Trail and Error
The python script vm.py defines a class named VM with the following constructor:
def **init**(self, rom):
self.rom = rom
self.accumulator1 = 0
self.accumulator2 = 0
self.instruction_pointer = 1
self.stack = \[\]
The VM stores the program code in the variable self.rom. It is filled on creation by reading the source file (program) given as argument.
The source is stored as a list (returned by .read().split() of a file object).
Two accumulator registers, self.accumulator1 and self.accumulator2, are initialized with ‘0’.
A third register is the self.instruction_pointer, it will the VM which operation in self.rom will be executed next.
It starts at ‘1’ and not at ‘0’.
The list containing the ROM is initialized with an empty string (['']) and then extended by the program code.
The last variable is self.stack which is empty list.
Lists in Python can be used as a stack like structure.
With list.append() (push) and list.pop() (pop) the behavior of these data structures is identical.
I decided to translate the emoji code of program into a more human readable version as a beginning.
A dictionary of all operations is at the bottom of the code.
The first version of my script did not translate all emojis in the code.
I started digging around further in vm.py to find some more emojis I had to consider.
As a result a almost completely emoji free version of the program could be generated.
The “final” version of my script emoji2mnemonic.py (Sorry got lost) had the following dictionary to translate program.
OPERATIONS = {
'🍡': 'add',
'🤡': 'clone',
'📐': 'divide',
'😲': 'if_zero',
'😄': 'if_not_zero',
'🏀': 'jump_to',
'🚛': 'load',
'📬': 'modulo',
'⭐': 'multiply',
'🍿': 'pop',
'📤': 'pop_out',
'🎤': 'print_top',
'📥': 'push',
'🔪': 'sub',
'🌓': 'xor',
'⛰': 'jump_top',
'⌛': 'exit',
'✋': ';',
'🥇': '[acc=1]',
'🥈': '[acc=2]',
'💰': '@',
'😐': 'end_if',
'🖋': 'func_',
'🏀': 'BRK<',
'⛰': 'BRK!',
'💠🔶🎌🚩🏁': 'Label01',
'💠🏁🎌🔶🚩': 'Label02',
'🚩💠🎌🔶🏁': 'Label03',
'🏁🚩🎌💠🔶': 'Label04',
'🔶🎌🚩💠🏁': 'Label05',
'🎌🏁🚩🔶💠': 'Label06',
'🔶🚩💠🏁🎌': 'Label07',
'🚩🔶🏁🎌💠': 'Label08',
'🎌🚩💠🔶🏁': 'Label09',
'🎌🏁💠🔶🚩': 'Label10',
'🏁💠🔶🚩🎌': 'Label11',
'💠🎌🏁🚩🔶': 'Label12',
'0️⃣ ': '0',
'1️⃣ ': '1',
'2️⃣ ': '2',
'3️⃣ ': '3',
'4️⃣ ': '4',
'5️⃣ ': '5',
'6️⃣ ': '6',
'7️⃣ ': '7',
'8️⃣ ': '8',
'9️⃣ ': '9',
}
The language for vm.py also knows labels for the jump_to operations and a symbol to distinguish between the accumulators to use.
A look at the translated source was a little bit more helpful. The example below shows a cleaned up, but shortened version of my interpretation of the syntax after translation.
load [acc=1] 0;
push [acc=1]
load [acc=1] 17488;
push [acc=1]
load [acc=1] 16758;
push [acc=1]
load [acc=1] 16599;
push [acc=1]
load [acc=1] 16285;
...
push [acc=1]
load [acc=2] 1;
func Label01
pop [acc=1]
push [acc=2]
push [acc=1]
load [acc=1] 389;
push [acc=1]
push [acc=2]
jump_to $[ Label04
xor
print_top
load [acc=1] 1;
push [acc=1]
add
pop [acc=2]
if_not_zero
jump_to $[ Label01
end_if
...
To find out what each operation does, I looked at the source code of vm.py.
The load instruction reads as follows: “Load accumulator1 with the immediate value 0”.
With push the value stored in the accumulator1 is pushed to the stack.
Other operations take the top two items from the stack to process them (addition, subtraction, multiplication, division, modulo, xor, …).
By only looking at the code I had no clue what was going on, but with all the jumps, I though about visualizing the program flow. I used my translated program and formatted the code to be a compatible Graphviz dot file. The resulting graph was again a little bit more of an help.
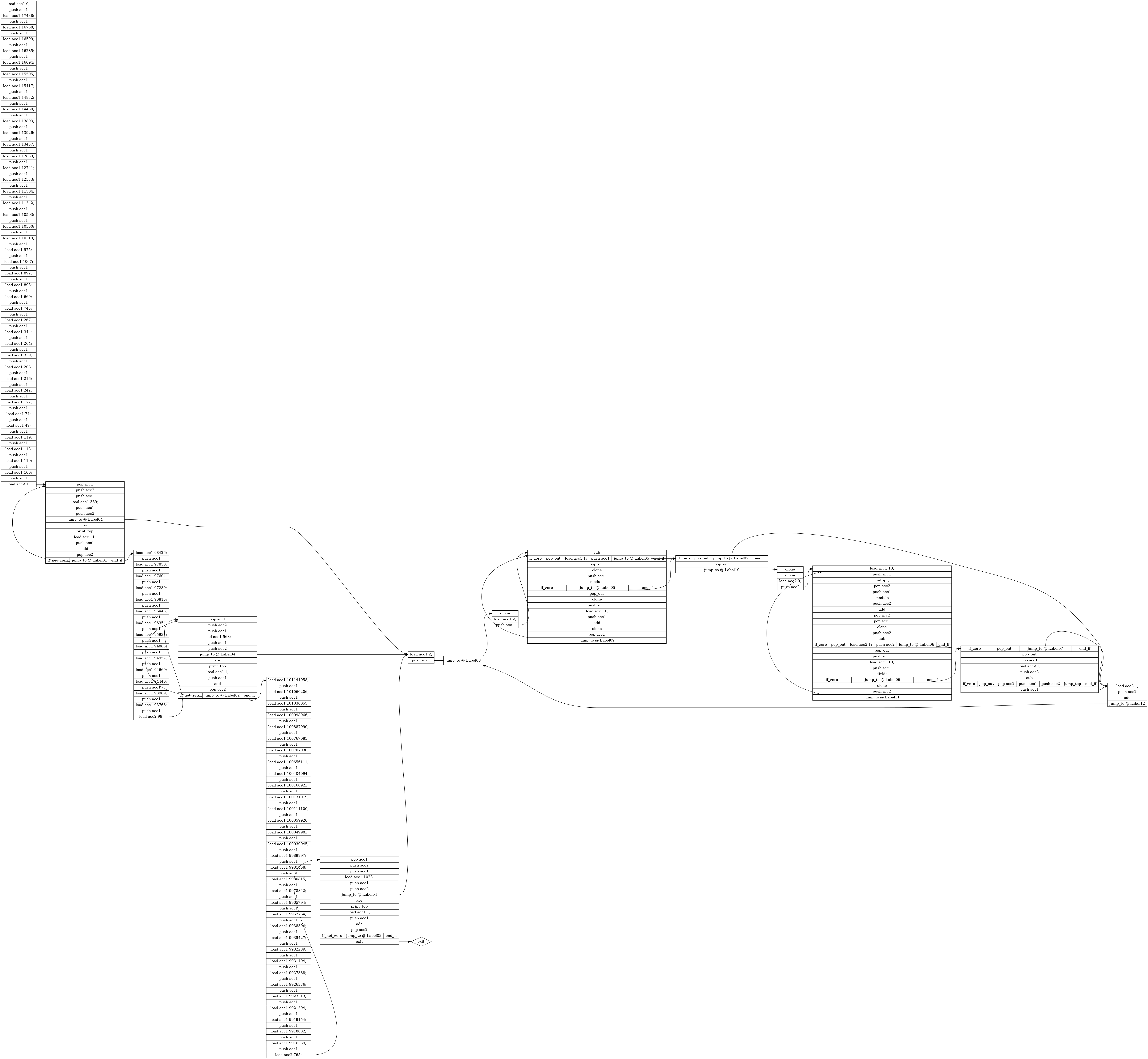
The graph shows a bunch of instructions to fill the stack of the VM. The right side has some more “complicated” instructions with modulo, division, xor, ….
When I see xor instructions, I often think of encryption and with multiplications and modulo instructions right next to it this though hardens.
But starring at the graph and the translated code did not help.
Solving the Challenge: Finally
It took me a while of starring until I realized, that I should try something else.
My next approach to solve this challenge was to write a trace log of the program execution step by step.
In each instruction function in vm.py I added some additional code to store the current status of the registers self.instruction_pointer, self.accumulator1, self.accumulator2 and translated each operation into its human readable counter part.
I also added (if possible) the parameters and the result of calculations.
00000002 [acc1=00000000][acc2=00000000]: load("acc1", 0)
00000006 [acc1=00000000][acc2=00000000]: push(acc1) = 0
00000008 [acc1=00017488][acc2=00000000]: load("acc1", 17488)
00000016 [acc1=00017488][acc2=00000000]: push(acc1) = 17488
00000018 [acc1=00016758][acc2=00000000]: load("acc1", 16758)
00000026 [acc1=00016758][acc2=00000000]: push(acc1) = 16758
00000028 [acc1=00016599][acc2=00000000]: load("acc1", 16599)
00000036 [acc1=00016599][acc2=00000000]: push(acc1) = 16599
00000038 [acc1=00016285][acc2=00000000]: load("acc1", 16285)
...
00000386 [acc1=00000389][acc2=00000001]: push(acc2) = 1
00000388 [acc1=00000389][acc2=00000001]: jump_to(Label04) @1040
00001041 [acc1=00000002][acc2=00000001]: load("acc1", 2)
00001045 [acc1=00000002][acc2=00000001]: push(acc1) = 2
00001048 [acc1=00000002][acc2=00000001]: jump_to(Label08) @1098
00001099 [acc1=00000002][acc2=00000001]: clone() = 2
00001100 [acc1=00000002][acc2=00000001]: load("acc1", 2)
00001104 [acc1=00000002][acc2=00000001]: push(acc1) = 2
00001107 [acc1=00000002][acc2=00000001]: sub(b=2, a=2) = 0
00001108 [acc1=00000002][acc2=00000001]: if_zero() = 0
00001109 [acc1=00000002][acc2=00000001]: pop_out() // 0
00001110 [acc1=00000001][acc2=00000001]: load("acc1", 1)
00001114 [acc1=00000001][acc2=00000001]: push(acc1) = 1
00001115 [acc1=00000001][acc2=00000001]: end_if = 🏀
00001115 [acc1=00000001][acc2=00000001]: …cont… if_zero()
00001116 [acc1=00000001][acc2=00000001]: jump_to(Label05) @1050
00001051 [acc1=00000001][acc2=00000001]: if_zero() = 1
00001055 [acc1=00000001][acc2=00000001]: end_if
00001057 [acc1=00000001][acc2=00000001]: pop_out() // 1
...
There are still a few emojis left, but I did not care about them.
With the trace log I could observe the program being executed and calculating the URL, or at least see the trace part where the print_top of the characters happens.
00001076 [acc1=00000002][acc2=00000001]: if_zero() = 0
00001077 [acc1=00000002][acc2=00000001]: pop_out() // 0
00001078 [acc1=00000002][acc2=00000389]: pop(acc2) = 389
00001080 [acc1=00000002][acc2=00000389]: push(acc1) = 2
00001082 [acc1=00000002][acc2=00000389]: push(acc2) = 389
00001083 [acc1=00000002][acc2=00000389]: end_if = ⛰
00001083 [acc1=00000002][acc2=00000389]: …cont… if_zero()
**00001084 [acc1=00000002][acc2=00000389]: jump_top() @389
00000390 [acc1=00000002][acc2=00000389]: xor(b=106, a=2) = 104**
00000391 [acc1=00000002][acc2=00000389]: print_top("h")
00000392 [acc1=00000001][acc2=00000389]: load("acc1", 1)
00000396 [acc1=00000001][acc2=00000389]: push(acc1) = 1
00000398 [acc1=00000001][acc2=00000389]: add(a=1, b=1) = 2
00000399 [acc1=00000001][acc2=00000002]: pop(acc2) = 2
00000401 [acc1=00000001][acc2=00000002]: if_not_zero() = 119
00000401 [acc1=00000001][acc2=00000002]: end_if = 🏀
00000401 [acc1=00000001][acc2=00000002]: …cont… if_zero()
00000402 [acc1=00000001][acc2=00000002]: jump_to(Label01) @371
The print_top instruction takes the item from the top of the stack and prints it out.
The stack only stores numbers, so the number is converted into a character before output.
Right before the print_top is a xor.
The xor takes the two top items from the stack to get the result of ‘104’ which is the letter “h”.
The number ‘106’ was pushed to the stack in the beginning, but where does the ‘2’ come from?
This took be a while to find out. But only after letting the program run bit longer.
$ grep -A1 xor trace.log
00000390 [acc1=00000002][acc2=00000389]: xor(b=106, a=2) = 104
00000391 [acc1=00000002][acc2=00000389]: print_top("h")
00000390 [acc1=00000003][acc2=00000389]: xor(b=119, a=3) = 116
00000391 [acc1=00000003][acc2=00000389]: print_top("t")
00000390 [acc1=00000005][acc2=00000389]: xor(b=113, a=5) = 116
00000391 [acc1=00000005][acc2=00000389]: print_top("t")
00000390 [acc1=00000007][acc2=00000389]: xor(b=119, a=7) = 112
00000391 [acc1=00000007][acc2=00000389]: print_top("p")
00000390 [acc1=00000011][acc2=00000389]: xor(b=49, a=11) = 58
00000391 [acc1=00000011][acc2=00000389]: print_top(":")
00000390 [acc1=00000101][acc2=00000389]: xor(b=74, a=101) = 47
00000391 [acc1=00000101][acc2=00000389]: print_top("/")
00000390 [acc1=00000131][acc2=00000389]: xor(b=172, a=131) = 47
00000391 [acc1=00000131][acc2=00000389]: print_top("/")
00000390 [acc1=00000151][acc2=00000389]: xor(b=242, a=151) = 101
00000391 [acc1=00000151][acc2=00000389]: print_top("e")
00000390 [acc1=00000181][acc2=00000389]: xor(b=216, a=181) = 109
00000391 [acc1=00000181][acc2=00000389]: print_top("m")
00000390 [acc1=00000191][acc2=00000389]: xor(b=208, a=191) = 111
00000391 [acc1=00000191][acc2=00000389]: print_top("o")
00000390 [acc1=00000313][acc2=00000389]: xor(b=339, a=313) = 106
00000391 [acc1=00000313][acc2=00000389]: print_top("j")
00000390 [acc1=00000353][acc2=00000389]: xor(b=264, a=353) = 105
00000391 [acc1=00000353][acc2=00000389]: print_top("i")
00000390 [acc1=00000373][acc2=00000389]: xor(b=344, a=373) = 45
00000391 [acc1=00000373][acc2=00000389]: print_top("-")
00000390 [acc1=00000383][acc2=00000389]: xor(b=267, a=383) = 116
00000391 [acc1=00000383][acc2=00000389]: print_top("t")
Again after a long round of starring at the output, it hit me.
The argument a is always a prime number, but these are special primes.
All primes are palindromes. The argument b is the value from the stack.
In my next step I wrote a script to calculate the palindrome primes and xor them with the values from the stack. I also discarded the idea to optimize the one of the components to solve this challenge.
As my final solution does not use the next code blocks anymore I will only highlight some ideas and problems I encountered.
I found a algorithm to calculate palindrome prime numbers on Stackoverflow and modified it to my needs.
def gen_pal_prime(a, b):
for i in range(a, b):
y = True
if str(i) == str(i)[::-1]:
if(i > 2):
for a in range(2, i):
if i % a == 0:
y = False
break
if y:
yield i
palindromes = [_ for _ in gen_pal_prime(0, 999999)]
The problem with this was, depending on the second parameter it takes a long time to calculate all primes and the other problem was, it did not work. Or it stopped working after the 39th character.
The algorithm failed to calculate the correct xor value for ‘93766’. As the string read until it broke “http://emoji-t0anaxnr3nacpt4na.web.ctfco” my guess was, that the next character has to be a ’m’ (ctfcompetition).
Brute forcing the prime number for ‘93766’ returned ‘93739’. What left me puzzled again. The previous prime number was ‘17471’. So I split up the whole blocks of pushing numbers to the stack into three blocks.
+-----------+-----------+-----------+
| Block 1 | Block 2 | Block3 |
+-----------+-----------+-----------+
| 17488 | 98426 | 101141058 |
| 16758 | 97850 | 101060206 |
| 16599 | 97604 | 101030055 |
| 16285 | 97280 | 100998966 |
| 16094 | 96815 | 100887990 |
| 15505 | 96443 | 100767085 |
| 15417 | 96354 | 100707036 |
| 14832 | 95934 | 100656111 |
| 14450 | 94865 | 100404094 |
| 13893 | 94952 | 100160922 |
| 13926 | 94669 | 100131019 |
| 13437 | 94440 | 100111100 |
| 12833 | 93969 | 100059926 |
| 12741 | 93766 | 100049982 |
| 12533 | 99 | 100030045 |
| 11504 | | 9989997 |
| 11342 | | 9981858 |
| 10503 | | 9980815 |
| 10550 | | 9978842 |
| 10319 | | 9965794 |
| 975 | | 9957564 |
| 1007 | | 9938304 |
| 892 | | 9935427 |
| 893 | | 9932289 |
| 660 | | 9931494 |
| 743 | | 9927388 |
| 267 | | 9926376 |
| 344 | | 9923213 |
| 264 | | 9921394 |
| 339 | | 9919154 |
| 208 | | 9918082 |
| 216 | | 9916239 |
| 242 | | 765 |
| 172 | | |
| 74 | | |
| 49 | | |
| 119 | | |
| 113 | | |
| 119 | | |
| 106 | | |
| 1 | | |
+-----------+-----------+-----------+
The purpose of the last number of each block opened up to me, when I finally found the correct prime for the third block. To decode the correct URL I ignored these numbers (‘1’, ‘99’, ‘765’) and started building special cases into my decoding function.
The code below almost worked fine.
Each block would be separately being decoded, after a certain number of iterations (i).
I tried to make some sense of these numbers at the bottom of each block.
print('Palindrome Primes #1')
palindromes1 = [_ for _ in gen_pal_prime(1, 18000)]
palindromes1.insert(0, 2) # manually add the number 2.
print('Palindrome Primes #2')
palindromes2 = [_ for _ in gen_pal_prime(93766 - 99, 999999)]
print('Palindrome Primes #3')
palindromes3 = [_ for _ in gen_pal_prime(9916239 - 765, 19916239)]
palindromes = palindromes1
stack.reverse()
for i, val in enumerate(stack):
if i == 40:
mode = 'stack2'
palindromes = palindromes2
if mode == 'stack2':
i -= 40
if i == 14:
mode = 'stack3'
palindromes = palindromes3
if mode == 'stack3':
i -= 13
c = val ^ palindromes[i]
print(f'{i:<8d}| {val:8d} ^ {palindromes[i]:<8} = {c:3d}', chr(c))
While my program ran, I encountered yet again a problem but this time during decoding the third block of numbers. The calculation of my palindrome primes took quite some time and did not result in printable/human readable characters.
Talking to a colleague of mine, he came up with the idea to look up lists of precalculated prime numbers and I found a website which provides lists of the first 2 billion prime numbers as downloadable files.
The site http://www.primos.mat.br/2T_en.html provides individual compressed text files, with 10 million primes each file. For this challenge the prime numbers from 2 to 179424673 should suffice.
After decompressing the file I had to convert the file from columns separated by tabs to a easier to read format for my Python programs.
To remove the columns and only have one prime per line I used the program tr.
$ tr 't' 'n' < 2T_part1.txt > primes.txt
I wrote a function to read this file to only return the palindrome primes as a list.
The str(_.rstrip()) == str(_.rstrip())[::-1] part of the condition will check if the number is a palindrome, by comparing the number as string against it reversed counterpart.
def load_primes(filename):
with open(filename, 'rt') as handle:
return [int(_) for _ in handle.readlines()
if str(_.rstrip()) == str(_.rstrip())[::-1]]
With this list of palindrome primes I wrote a short brute force solution to find the correct prime number to decode the third block, or to be more precise, where in this list of primes can I find it.
As a constraint I iterated through all primes until the prime p from primes is greater than the number (‘9916239’) I am looking for.
Then I know, that my prime had to be within the first 765 primes.
>>> primes = solver.load_primes('primes.txt')
>>> for i, p in enumerate(primes):
... if p > 9916239:
... print(i)
... break
...
765
At this point the 3 numbers I could not figure out until now. These are the n-th number prime from a list of consecutive palindrome primes. The first block begins at the the 1st prime from my list of primes, the second block begins at the 99th prime number and the third block at the 765th prime number from my list.
And now it also makes sense, why program becomes slower with each iteration.
The code block (see the call graph above) calculates palindrome prime numbers, which becomes more and more of a problem regarding performance when it hits greater numbers.
How does my final solution look like? I wrote a script called solver.py, put all numbers from all three blocks into a single list and wrote my decryption function.
#! /usr/bin/env python
#-*- coding: utf-8 -*-
stack = [101141058, 101060206, 101030055, 100998966, 100887990,
100767085, 100707036, 100656111, 100404094, 100160922,
100131019, 100111100, 100059926, 100049982, 100030045,
9989997, 9981858, 9980815, 9978842, 9965794, 9957564,
9938304, 9935427, 9932289, 9931494, 9927388, 9926376,
9923213, 9921394, 9919154, 9918082, 9916239, # Block 3
98426, 97850, 97604, 97280, 96815, 96443, 96354, 95934,
94865, 94952, 94669, 94440, 93969, 93766, # Block 2
17488, 16758, 16599, 16285, 16094, 15505, 15417, 14832,
14450, 13893, 13926, 13437, 12833, 12741, 12533, 11504,
11342, 10503, 10550, 10319, 975, 1007, 892, 893, 660,
743, 267, 344, 264, 339, 208, 216, 242, 172, 74, 49, 119,
113, 119, 106] # Block 1
def load_primes(filename):
with open(filename, 'rt') as handle:
return [int(_) for _ in handle.readlines()
if str(_.rstrip()) == str(_.rstrip())[::-1]]
if __name__ == '__main__':
palindromes = load_primes('primes.txt')
stack.reverse()
offset = 0
for i, val in enumerate(stack):
if i == 40:
offset = 98 - 40
if i == 54:
offset = 764 - 54
c = val ^ palindromes[i + offset]
print(chr(c), end='')
print()
Running this script will produce the URL “http://emoji-t0anaxnr3nacpt4na.web.ctfcompetition.com/humans_and_cauliflowers_network/”.
Visiting this URL gives a choice for three sub pages of different people.
The flag is stored in the personal page of Amber within a picture.
The flag reads “CTF{Peace_from_Cauli!}”.
Lessons learned
Doing CTFs sometimes require you to think out of the box and/or ignore the first possible solutions which might seem to be the obvious ones, but might lead you nowhere or are just there to keep you side tracked.
This challenge first got me thinking about modifying and changing the behavior of the provided files program and vm.py.
While working through the challenge, which kept me busy for quite some time, I found a different solution.
The previous tries to solve this challenge were not for nothing, especially the addition of my trace log addition, which finally helped me understanding the problem and getting my on the right track to the solution.